- Home
- Products
- ARM
- Frequently Asked Questions
- Summarizing
ARM Frequently Asked Questions: Summarizing
Why do treatment means have 'na' instead of mean comparison letters?
Why do treatment means have 'na' instead of mean comparison letters?
Starting in ARM 2024.1, AOV reports may use 'na' instead of mean comparison letters for certain assessment columns. This is accompanied by a footnote stating "Mean separation letters are 'na' (not applicable) when error variance is 0." There are two scenarios where this can occur.
Scenario 1: All observations are the same value
The first scenario is when an entire assessment has no variation in the observations, commonly all 0s or 100s when there is no pest presence or zero damage to the crop, for example.
In this situation there is 0 variability in the data set, and when there is no variance, ARM cannot perform an Analysis of Variance! Technically, the sum of squares calculation is 0, and thus the error mean square is 0. So no F statistic can be calculated for AOV (and so is reported as 'NaN' for "not a number"). Because no further analysis can be performed, ARM displays "na" to make it clear that no statistical conclusions can be drawn from this data because a statistical analysis was not performed.
Scenario 2: Differences among treatments but no differences across replicates
The second scenario is when an assessment has no variation across replicates within treatment, even though numerical differences exist between different treatments. For example, a "percent control" rating where the check is 0, but all other treatments completely controlled the pest, so all observations are 100. Or a visual assessment was performed that aggregates the entire treatment across replicates; we will use a general phytotoxicity example here:
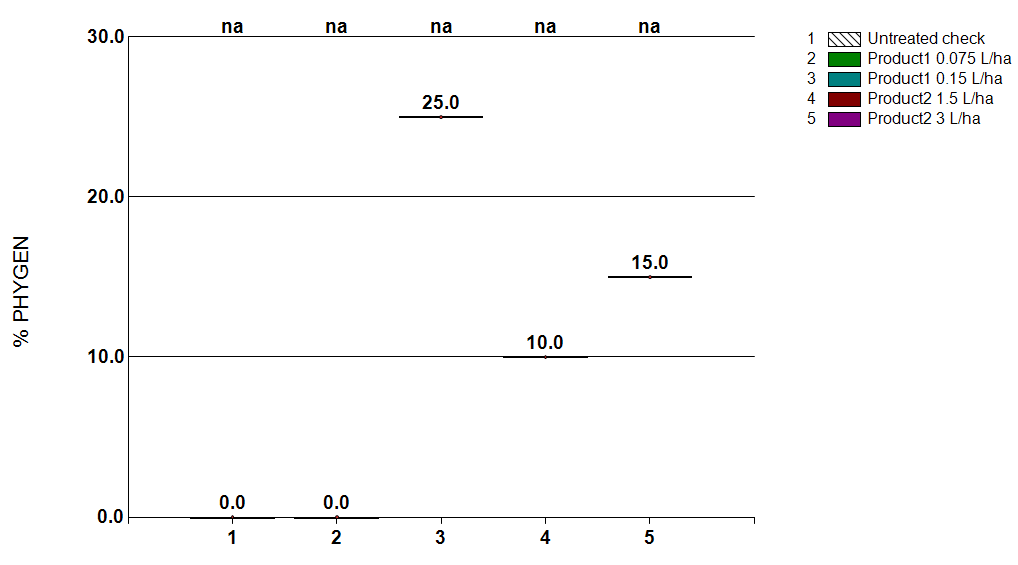
There is variation across treatments in this situation, but 0 variability within each treatment. In the AOV table below, although the Sum of Squares is not zero, the error mean square is once again 0, and so there is no result from AOV:
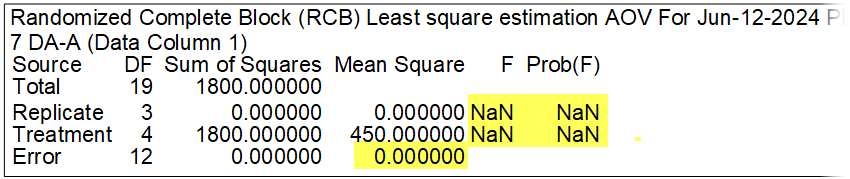
So, like in Scenario 1 above, ARM displays 'na' to indicate that no statistical conclusions can be drawn from this data because a statistical analysis was not performed.
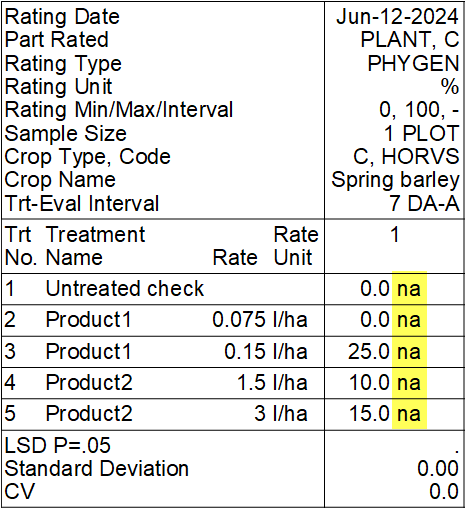
Another way to look at this scenario is to consider that each treatment reall has only one observation. Although there is replication in the study, for this particular assessment the observation was identical for every experimental unit (or like in our example the rating is an average across all replicates, and simply entered into ARM as replicated data). Thus, this assessment is like a one-replicate study or an observational rating, which cannot be analyzed using statistics.
A couple of points of emphasis:
- The 'na' does not mean "no significance." It means "we cannot calculate statistical significance."
- This does not mean the data has no value, just that statistical conclusions are not possible for this assessment.
Can we change this back?
No. ARM reports are now clearer and more accurate in the above scenarios, and we cannot, in good faith, return to a statistically misleading output.
This change has prompted many questions from ARM users, both for their own understanding as well as their clients. The conversations GDM has had with clients on this topic have been positive. Thus, we are confident the authorities and other clients will come to understand the situation, too, and trial results will be shared more accurately and understood better as a result of this change. In fact, a regulatory group brought this issue to our attention in the first place!
In summary, statistical conclusions cannot be drawn from the type of ratings described above. ARM reports now make this clear and evident, carrying on the tradition that ARM ensures the presentation of the research data is not misleading.
How do I control the number of decimals for summary means in Summary reports?
How do I control the number of decimals for summary means in Summary reports?
By default, ARM reports one more decimal of accuracy on means than the most precise data point entered in a data column. For example, if the data points of 36, 45, and 98.02 are entered in a data column, ARM reports three decimals of accuracy on the means.
There are two methods to control or force the number of decimals accuracy.
Method 1: Apply to all columns
To set the number of decimals for all columns on the report, use the 'Force Number of Decimals Accuracy to' option on the General Summary Report Options window. Using this option, you may enter the number of decimals to use on summary reports when there is no entry for an assessment column in the assessment data header Number of Decimals field (see next method).
Note: Forcing number of decimals to 0 or 1 in General Summary Report Options is very likely to hide important differences for small treatment means, such as yield values less than 25.
Method 2: Apply to columns differently
To override a default set by method 1, enter the number of decimals of accuracy desired in the Number of Decimals assessment data header for each data column. Enter a "0" to force means to print as whole number with no decimals reported.
The number of decimals field is located at the bottom of assessment data header (in the Miscellaneous group). If you cannot see the Number of Decimals field on the screen, then check whether this field is hidden in the current Assessment Data View. Select Tools > Options > Assessment Data View, and be sure that Visible is checked for the Number of Decimals field.
Why do some treatment means have the same mean comparison letter when the difference between means is larger than the reported LSD?
Why do some treatment means have the same mean comparison letter when the difference between means is larger than the reported LSD?
Duncan's MRT, Student-Newman-Keuls, and Tukey's tests do not separate means the same as LSD. The mean comparison tests included in ARM are LSD, Duncan's MRT (called Duncan's New Multiple Range Test), Student-Newman-Keuls, Tukey's, Waller-Duncan, and Dunnett's. Mean comparisons based on LSD have often been criticized because the significance level "slips" when the number of treatments increases. (See 'AOV Means Table Report Options' in ARM Help for more information on mean comparison tests.)
If a group of treatment means are sorted in order from high to low, then Duncan's and LSD give approximately the same result for adjacent pairs of treatment means. (Adjacent pairs of treatment means are those beside each other when sorted in order from high to low.)
With Duncan's and Student-Newman-Keuls, the minimum value for significance becomes larger for mean pairs that are farther apart in the sorted list.
Both LSD and Tukey's use the same value for all tests, but the Tukey's value is quite large when compared to the LSD. (Thus, there are fewer significant differences.)
To use LSD as the mean comparison test in ARM (or to change mean comparison method):
To use LSD as the mean comparison test in ARM (or to change mean comparison method):
- Select File - Print Reports from the ARM menu bar.
- Double-click on the Summary heading in the left column that lists available reports to expand the list of available summary reports.
- Click once on AOV Means Table in the left column so this choice is highlighted.
- Click the Options button below the list of available reports to display the AOV Summary Report Options.
- Click the down pointing arrow following the mean comparison test method. Select LSD to use this test method.
- The F1 help also provides additional information on the mean comparison test methods.
Following is information about LSD extracted from 'AOV Means Table Report Options' in ARM Help:
When using LSD to make an unplanned comparison of the highest and lowest mean in a trial with more than two treatments, the difference between treatments can be substantial even when there is no treatment effect. For example, when using a 5% significance level the actual significance level is larger than 5%. Some statisticians have determined that for a trial with three treatments the significance level is actually 13%, for six treatments the significance level is 40%, for 10 treatments the significance level is 60%, and for 20 treatments the significance level is 90%.
[William G. Cochran and Gertrude M. Cox, Experimental Designs, 2nd edition (New York, John Wiley and Sons, Inc, 1957).]
There is also an AOV Means Table Report option set that is making "protected" mean comparison tests: the option to run mean comparison test "Only when significant AOV treatment P(F)". When this option is active, ARM will not report any differences as significant when the treatment probability of F is greater than the mean comparison significance level, for example 0.10 (or 10%). The statement that "Mean comparisons performed only when AOV Treatment P(F) is significant at mean comparison OSL." is printed as a report footnote when this option is active.
There is also an AOV Means Table Report option set that is making "protected" mean comparison tests: the option to run mean comparison test "Only when significant AOV treatment P(F)". When this option is active, ARM will not report any differences as significant when the treatment probability of F is greater than the mean comparison significance level, for example 0.10 (or 10%). The statement that "Mean comparisons performed only when AOV Treatment P(F) is significant at mean comparison OSL." is printed as a report footnote when this option is active.
Why do all treatment means have 'a' or '-' as the mean comparison letter?
Why do all treatment means have 'a' or '-' as the mean comparison letter?
Even though there may be considerable differences between means, it is possible that ARM lists 'a' or a dash '-' as the mean comparison letter for all treatments for a particular column on the AOV Means Table report. This can occur when running a "protected" mean comparison test, which is a statistically-recommended practice.
Selecting the option Only when significant AOV treatment P(F) on the AOV Means Table Report options enables the 'protected' mean comparisons. This means that if the AOV test statistic F is not significant (i.e. Treatment P(F) > signficance level), ARM does not perform mean comparisons. If this occurs, ARM displays the mean comparison symbol defined in the Symbol indicating no significant difference between treatment means AOV report option instead of the mean comparison letter, which is a dash '-' by default. And if this option is blank, ARM displays 'a' beside all treatment means, which can appear as though a mean comparison was run with no differences found.
So, if all treatment means have 'a' as the mean comparison letter even when it appears that differences should have been found, it is because the AOV treatment P(F) indicates that at the specified significance level, there is no statistical evidence supporting the AOV alternative hypothesis that "at least one treatment is different." Thus, there is no evidence to reject the null hypothesis that "all treatments are the same," and no reason to perform mean comparisons.
Why are treatment means of transformed data different than means of the original untransformed data?
Why are treatment means of transformed data different than means of the original untransformed data?
The reason there is a difference between the means of the transformed replicates when compared with the means of the raw data is because the means of transformed data are "weighted means". ARM performs Analysis of Variance on the transformed data values, calculates the treatment mean from the transformed values, then de-transforms the treatment means so they can be reported in the original units. (Means reported as log, square root, or arcsine percent values are very difficult to understand.)
The reason why the weighted means are different than the raw data means relates to the reason why the data must be transformed. A detailed explanation of the reason depends on which transformation was used.
Following is a description of the reason for this difference with data that has been transformed using square root. The description is from page 156 of the "Agricultural Experimentation Design and Analysis" book by Thomas M. Little and F. Jackson Hills, published 1978 by John Wiley and Sons. The discussion is regarding insect count data that was not normally distributed because many of the insect counts were very low - instead the data followed a Poisson distribution. The data was transformed and analyzed, means were calculated from the transformed values, then detransformed to the original units.
"The means obtained in this way are smaller than those obtained directly from the raw data because more weight is given to the smaller variates. This is as it should be, since in a Poisson distribution the smaller variates are measured with less sampling error than the larger ones."
Another way to say this is "The weighted means are more correct because the means are calculated from data where the original heterogeneity problem has been fixed."
Note: To include the "raw" arithmetic mean on the report for reference, turn on the Arithemetic Mean option under Mean Descriptions section in the AOV Means Table report options.These means are placed separate from the statistical values because statistical results are not based on the arithmetic means.
What should I do if my data does not meet the assumptions of AOV?
What should I do if my data does not meet the assumptions of AOV?
There are several assumptions that the AOV analysis makes about the data in order to draw conclusions. The two assumptions that ARM tests for are:
- Normality – the distribution of the observations must be approximately normal, or bell-shaped. Simply put, most of observations will be relatively near the mean, so we can reasonably expect to not have major outliers. The measurements to test this assumption in ARM, which can be included on reports by selecting the respective AOV Means Table option, are:
- Skewness – a measure of how symmetrical the observed values are.
- Kurtosis – a measure of how ‘peaked’ the data is (how ‘flat’ or ‘pointed’ relative to the normal distribution).
- Shapiro-Wilks – a general statistical test for normality
- Homogeneity of variances – the variability of observations are approximately equal regardless of which treatment was applied. The mean comparison tests rely heavily on this assumption, since the tests are carried out using a common variance from all treatments.
- Levene's or Bartlett's – a statistical test for homogeneity of variance. When the data is reasonably normally-distributed, Levene's and Bartlett's tests are comparable. But when the data is non-normal or skewed, Levene's test provides better results than Bartlett's, and so Levene's test is the recommended option overall.
- The Box-Whisker graph is a great tool to visually investigate and demonstrate this concept. Boxes that are of similar height and shape across all treatments in a data column indicate homogenous variances.
If these assumptions are not met, the resulting analysis may be completely invalid:
“Failure to meet one or more of these assumptions affects both the level of significance and the sensitivity of the F test in the analysis of variance [AOV].” (Gomez and Gomez; Statistical Procedures for Agricultural Research pp.294-295).
There are a few things a researcher can try in order to “correct” the data to fit the assumptions of AOV. It should be stressed that these techniques are not “fudging” the data, but rather applying statistically-sound, industry-standard processes in order to compare the treatment means to get the mean comparison letters on the report. With ARM, these techniques can be automatically suggested using the Column Diagnostics panel - view this tutorial video to learn how to use this tool.
- Apply automatic transformation – ARM can apply one of the following automatic data correction transformations:
- Square root (AS) – often used with ‘count’ rating types (e.g. # of insects per plant).
- Arcsine square root percent (AA) – used with counts taken as percentages/proportions.
- Log (AL) – can only be used for non-negative numbers.
The purpose of applying a transformation is to work with data that fits the assumptions of AOV – a transformation often fixes non-normality and/or non-homogeneity of variances by reducing the scale of the data. Note that it can be statistically and mathematically proven that:
“because a common transformation scale is applied to all observations, the comparative values between treatments are not altered and comparisons between them remain valid.” (Gomez and Gomez; Statistical Procedures for Agricultural Research pp.299)
Since the transformed data and resulting means will be on a different scale, use the “De-transform means” option on the General Summary report options to de-transform the means into the original units. Note that this does not affect any results.
- Non-parametric statistics – When none of the data correction transformations resolve the failed assumptions, use the Action Code 'AR' to perform non-parametric statistics for that assessment. These are rank-based statistical routines that do not rely on AOV and so are not affected by heterogeneity of variances or non-normality.
- Spatial analysis – Spatial analysis attempts to recover hidden spatial information. This analysis abandons the randomization design (e.g. RCB) and instead fits a statistical model to the data in an effort to recover information from hidden or difficult to measure variables in the field. View this presentation for more details on spatial analysis.
How does ARM calculate the Standard Deviation for the AOV Means Table report?
How does ARM calculate the Standard Deviation for the AOV Means Table report?
By definition, standard deviation is the square root of variance. The standard deviation reported by ARM is the square root of the Error Mean Square (EMS) from the AOV table. When trial data is analyzed as a randomized complete block (RCB), ARM performs a two way analysis of variance (AOV). As a result, both the treatment and the replicate sum of squares are partitioned from the error sum of squares.
Sometimes a user attempts to verify the standard deviation calculated in ARM by using Excel or a scientific calculator. It is important to note that the standard deviation calculated by a spreadsheet or a scientific calculator is typically based on a one way AOV. The EMS (and thus the standard deviation) calculated for a one way ANOVA is different than that calculated for a two way AOV, so standard deviation calculated by ARM for a RCB experimental design will almost always be different than the standard deviation calculated using a spreadsheet or scientific calculator. In other words, the variance (EMS) is not the same when calculated for a two way ANOVA as a one way ANOVA.
ARM performs a one way AOV only when analyzing trial data as a completely random experimental design. For a completely random design, the standard deviation calculated by Excel or a scientific calculator will match the one calculated by ARM.
What is the difference between Bartlett's and Levene's tests of homogeneity of variance?
What is the difference between Bartlett's and Levene's tests of homogeneity of variance?
On the AOV Means Table report, select the 'Homogeneity of variance test' descriptive statistic to print a test statistic and the significance level for the selected test of homogeneity of variance. The significance indicates the likelihood that data violates the assumption of homogeneity of variance. Thus, a probability of 0.05 indicates a 95% certainty that variances are heterogeneous.
When the data is reasonably normally-distributed, Levene's and Bartlett's tests are comparable, with a slight edge to Bartlett's. (Use the Skewness and Kurtosis statistics to test for normality.)
- If you have strong evidence that your data do in fact come from a normal, or nearly normal, distribution, then Bartlett's test has more statistical power.
However, Levene's test is less sensitive to departures from normality than Bartlett's. So if the Bartlett's test fails for a given column, it could be due to non-normality or heterogeneity of variance. But without evidence that the data is nearly normal, you cannot be certain that it is the heterogeneity of variance that the test is detecting.
- Thus when the data is non-normal or skewed, Levene's test provides better results.
Therefore Levene's test is the recommended option overall.
Reference:
Milliken and Johnson. Analysis of Messy Data. Chapman & Hall/CRC, 1992.
Dose-Response Analysis Report
Dose-Response Analysis Report
The dose-response analysis is used in experiments where a treatment or chemical is applied at different rates, and the level of response to the dosage is recorded (as a percentage or count of individuals that responded). The analysis estimates the treatment rate/dosage that results in a response from a particular percentage of individuals in the study. One example is the LD50, which estimates the dosage level that results in a response of 50%, i.e. the median lethal dose.
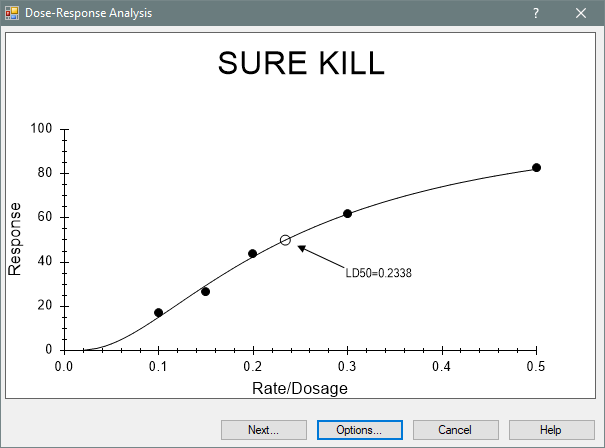
ARM provides three different Dose-Response estimation algorithms: Probit - Least Squares, Probit - Maximum Likelihood, and Logit. These algorithms were provided courtesy of Dr. J. J. Hubert, University of Guelph.
See Dose-Response Analysis Report (pdf) for information about printing this report.
